
UCR Applied Math
Field of applied mathematics includes development of novel and application of novel and existing mathematical and computational methods to physics, biology, medicine, engineering, data science, computer science, business, and industry.
Information & Resources
News & Announcements
The applied Math Group will host news and announcements here. Check back soon for updates. Thank you.
Applied Math Projects
Detailed Description of Research Projects with other UCR Departments, Universities, National Laboratories and Medical Schools
Collaborative Projects
Integrative multiscale modeling and multimodal experiments to decode systems-level molecular mechanisms of epithelial systems
Collaborators: Dr. Mark Alber, Dr. Weitao Chen, Dr. Amit K. Roy Chowdhury (all UCR), Dr. Jeremy Zartman and Dr. Alexander Dowling (U Notre Dame)
This project seeks to combine mathematical modeling and experimentation to bridge the critical knowledge gaps required to predict how molecular signaling controlled by morphogens such as the Bone Morphogenetic Protein (BMP) and Wing-less/WNT signaling pathways through cytoskeletal regulators drives cell and tissue shape generation and maintenance during embryo development. Members of the team will integrate breakthroughs in mathematical theory of reaction-diffusion PDE systems on extending and deforming manifolds coupled with coarse graining mechanistic modeling approaches describing cell membrane and cytoskeleton with machine learning based surrogate models for image analysis, parameter estimation and uncertainty analysis.
Combined Modeling and Experimental Study of the Mechanisms of Growth Patterns in Stem Cell Homeostasis in Plants
Collaborators: Dr. Mark Alber, Dr. Weitao Chen, Dr. G. Venugopala Reddy and Dr. Amit K. Roy Chowdhury (all UCR)
This interdisciplinary research program aims to understand how mechanical connections among cells and chemical signals between them collaborate to control the growth, sell-organization and differentiation of stem cells during plant growth. Mathematical and computer models will allow researchers to perform virtual experiments that are currently impossible in the lab. Coupled with live imaging experiments and new image analysis methods, these experiments will yield insights into biological mechanisms governing organ formation in plants and animals and development of cancer in epithelial cell layers of the colon.
DOE/PNNL/ORNL-UCR project: Elucidating Principles of Bacterial-Fungal Interactions
Collaborators: Dr. Mark Alber (all UCR), Dr. William Cannon (PNNL) and Dr. Dale Pelletier (ORNL)
The focus of this project is the development hybrid machine learning/simulation models of Pseudomonas uorescens/Laccaria bicolor interactions and dynamics. These hybrid data-analytic/simulation models will be used to carry out virtual experiments and develop fundamental understanding of the interactions between Pseudomonas uorescens and Laccaria bicolor. A fundamental understanding of how a property emerges from underlying processes is developed through understanding how the physics of underlying processes result in the emergent property. For instance, how do changes in energy metabolism and signaling by chemoattractants result in the sophisticated chemotactic searches for food? At the same time, experiments will be carried out aimed at developing and testing quantitative assays to measure the same interactions, and whose data will inform the virtual experiments.
Collaborative project with University of Pennsylvania School of Medicine: Multi-scale mathematical modeling and empirical study of mechanisms limiting blood clot growth
Collaborators: Dr. Mark Alber, Dr. Zhiliang Xu (U Notre Dame) and Dr. John Weisel (UPenn)
Thrombosis is a major cause of death in the developed world and results from the growth of thrombi (blood clots forming within blood vessels) that restricts blood flow to vital organs. The project integrates multi-scale mathematical modeling and experiments to examine novel hypothesis related to the role of fibrin networks in processes halting thrombus growth. This will help physicians to estimate risk of thrombotic disease for an individual patient by identifying critical values of parameters of processes regulating thrombogenesis.
Collaborative project with City of Hope National Medical Center: mathematical modeling of chemotaxis-driven migration of therapeutic neural stem cells to sites of tumors and injury
Collaborators: Dr. Heyrim Cho, Dr. Russell Rockne (City of Hope), and Dr. Margarita Gutova (City of Hope)
Neural stem cells (NSC) have been shown to be a safe and effective means of treatment of primary brain tumors as well as traumatic brain injury. NSCs have demonstrated tropism to remote sites of tumor or injury in the brain, and have also been shown to migrate along anisotropic white matter tracts. NSCs may be delivered through several routes of administration, including intracerebral, intrathecal, and intranasal injection. This project aims to use mathematical modeling of chemotaxis-driven migration combined with anatomical features of the brain to predict--and subsequently improve--the efficiency of administration of NSCs to sites of tumor or injury. The models will be calibrated from pre-clinical animal models and compared with data collected from patients treated at City of Hope.
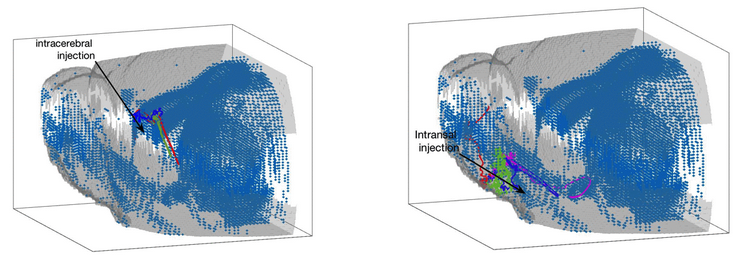
Collaborative project with City of Hope National Medical Center: mathematical modeling of hematopoiesis and leukemia from single-cell gene sequencing data
Collaborators: Dr. Heyrim Cho (UCR), Dr. Russell Rockne (City of Hope), and Dr. Ya-Huei Kuo (City of Hope)
Single-cell RNA sequencing data provides the gene expression level that is in the dimensionality of O(105) per each individual cell. By applying dimension reduction techniques, the data reveals a continuum of cell states that challenges the classical view of cell biology assuming discrete cell states. Continuum cell state models will be developed from single-cell RNA sequencing data to describe the trajectories in the continuum cell state space of hematopoiesis. The models will be used to study abnormal differentiation processes, e.g. acute myeloid leukemia progression, to predict the emergence of novel intermediate cell states, and used to investigate therapeutic targets.
Collaborative project with University of California, Irvine: Multi-Scale Modeling and Experimental Study of Hair Follicle Growth Control
Collaborators: Dr. Qixuan Wang (UCR), Dr. Maksim Plikus (UC Irvine)
Hair follicles are stem cell-rich skin mini-organs that can undergo oscillation-like cycles of regeneration throughout their lifetimes. In recent years, hair follicle has emerged as a leading model system for studying general mechanisms of stem cell control, tissue patterning during morphogenesis, regeneration and aging. Though powerful, traditional reductionist research approaches are limited by technological barriers and high experiment costs. This project aims to develop an interdisciplinary approach between computational modeling and experimentations to understand crucial questions that arise from the growth control of the follicle and stem cell lineage dynamics. It is anticipated that the new mathematical model developed in this project can be generalized to study multiple aspects of skin biology as well as other biological growth systems. (Supported by NSF DMS 1951184, DMS 1951144)
Interdisciplinary Investigation of Asthmatic Airway Remodeling
Collaborators: Dr. Qixuan Wang, Dr. Mark Alber (all UCR), Dr. Mona Eskandari (UCR, Mechanical Engineering, BREATHE Center)
Asthma is a serious health and socioeconomic issue all over the world, affecting more than 300 million individuals. In patients with asthma, the airway wall structure undergoes pathological modifications that include changes in the composition and organization of its cellular and molecular constituents, leading to the thickening and stiffening of the interstitial matrix in the innermost airway layer. These phenomena give rise to morphological remodeling resulting in lumen blockage. In this project, we develop multi-scale computational models to investigate the impact of fibrous network remodeling in asthma on the airway biomechanics and morphology. Model predictions are experimentally validated in Dr. Eskandari’s lab.
Underpinning Swimming Mechanisms of Eukaryotic Microorganisms via Computations and Analysis of PDEs
Collaborators: Dr. Qixuan Wang, Dr. Mykhailo Potomkin, Dr. Bhargav Rallabandi (UCR Mechanical Engineering)
At microscale, the main constituent of life on Earth is microorganisms. Examples are bacteria, spermatozoa, and other single-cell organisms. A biological cell typically uses flexible appendages, flagella and cilia, to propel itself in a fluidic environment. Flagellar beating is caused by activity of molecular motors (or so-called motor proteins) that bend the flagellum and result in life-like pulsating of the flagellum. In this project, we develop nonlinear PDE based multi-scale models that integrate molecular kinetics, flagellar beating and fluid-structure interaction. We also use techniques from numerical analysis, applied dynamical systems, elasticity and fluid dynamics to model and investigate the biophysical principles that lead to stable swimming dynamics of the cell.
Multidisciplinary University Research Initiative with University of Houston, University of Maryland, College Park, University of California, Los Angeles and Princeton University: Innovations in Mean-Field Game Theory for Scalable Computation and Diverse Applications
Collaborators: Dr. Wilfrid Gangbo (UCLA), Dr. Michele Gelfand (UMD) , Dr. Tom Goldstein (UMD), Dr. Zhu Han (U Houston), Dr. Dana Nau (UMD), Dr.Stanley Osher (UCLA), Dr. H. Vincent Poor (Princeton), Dr. Yat Tin Chow (UCR), Dr. Wuchen Li (U South Carolina), Dr. Alpar Richard Meszaros (Durham U), Dr. Penghang Yin (SUNY), Dr. Micah Goldblum (UMD), Dr. Flavien Leger (ENS Paris), Dr. Matt Jacobs (UCLA), Dr. Karthik Elamvazhuthi (UCLA), Dr. Daniel McKenzie (UCLA), Dr. Chenchen Mou (CityU of HK), Dr. Levon Nurbekyan (UCLA), Dr. Brian Swenson (Princeton), Dr. Honglian Zhang (Princeton)
Mean field games study strategic decision making in large populations where the individual players with each other and each individual is affected only by certain averaged quantities of all the other individuals. The mean field represents the behavior of a large number of agents by their population density function. This setting connects with optimal transport theory, Nelson's stochastic mechanics, partial differential equations, optimization, probability and statistics with applications in machine learning problems. This project aims to have a coordinated effort based on an overarching mathematical framework, accurate modeling in diverse applications, and a set of algorithmic tools that support fast simulation, prediction, and inverse design for mean field game, and is a collaborative effort of partial differential equations, numerical analysis, optimization, machine learning, psychology, artificial intelligence and game theory, and electrical engineering.
ICQMB
UC Riverside Interdisciplinary Center for Quantitative Modeling in Biology (ICQMB)
Many members of the Applied Mathematics Group are affiliated with the ICQMB and are collaborating with members of the Center from different departments and colleges: https://icqmb.ucr.edu/our-people
The main long-term goal of the ICQMB is to develop comprehensive predictive quantitative mathematical and computational models of complex biological systems. All projects at this center combine quantitative experiments; novel image analysis, modeling and statistical approaches, and builds upon the mutually complementary strength of the researchers at UC Riverside with support from collaborators at other institutions. The ICQMB organized large number of conferences on mathematical and computational biology: https://icqmb.ucr.edu/conferences
Publications
Mark Alber
- Ali Nematbakhsh, Megan Levis, Nilay Kumar, Weitao Chen, Jeremiah Zartman andMark Albre [2020], Epithelial organ shape is generated by patterned actomyosincontractility and maintained by the extracellular matrix, PLoS Computational Biology,16(8): e1008105. https://doi.org/10.1371/journal.pcbi.1008105
- Samuel Britton, Mark Alber and William R. Cannon [2020], Enzyme ActivitiesPredicted by Metabolite Concentrations and Solvent Capacity in the Cell, Journal of theRoyal Society Interface 17(171), 20200656.
- Oleg V. Kim, Rustem I. Litvinov, Mark S. Alber and John W. Weisel [2017],Quantitative Structural Mechanobiology of Platelet-Driven Blood Clot Contraction,Nature Communications 8: 1274. https://www.nature.com/articles/s41467-017-00885-x.pdf (authors for correspondence: J.W. Weisel and M. Alber).
- Special Issue on "Multi-scale Modeling of Tissue Growth and Shape", Bulletin of Mathematical Biology, Mark Alber, Christophe Godin, Philip Maini, Roeland Merks,Eric Mjolsness, Editors, Volume 81, Issue 8 (2019).
William Cannon
- Cannon, W. R., Zucker, J. D., Baxter, D. J., Kumar, N., Baker, S. E., Hurley, J. M. and Dunlap, J. C., Prediction of Metabolite Concentrations, Rate Constants and Post-translational Regulation using Maximum Entropy-based Simulations with Application to Central Metabolism of Neurospora crassa," Processes (2018) 6, 63, doi:10.3390/pr6060063.
- Alber, M., Buganza Tepole, A., Cannon, W.R. et al. Integrating Machine Learning and Multiscale Modeling—Perspectives, Challenges, and Opportunities in the Biological, Biomedical, and Behavioral Sciences. npj Digit. Med. 2, 115 (2019) doi:10.1038/s41746-019-0193-y
- Britton, S., Alber, M, and Cannon, W. R., Enzyme Activities Predicted by Metabolite Concentrations and Solvent Capacity in the Cell, Journal of The Royal Society Interface (2020), 17(171): 20200656, doi:10.1098/rsif.2020.0656
Weitao Chen
- Kevin Tsai, Samuel Britton, Ali Nematbakhsh, Roya Zandi, Weitao Chen*, Mark Alber* (2020). Role of combined cell membrane and wall mechanical properties regulated by polarity signals in cell budding. (* co-corresponding author) Physical Biology 17 065011.
- Xue Pan, Linjing Fang, Jianfeng Liu, Betul Senay-Aras, Wenwei Lin, Shuan Zheng, Tong Zhang, Jingzhe Guo, Uri Manor, Jaimie Van Norman, Weitao Chen*, Zhenbiao Yang* (2020). Auxin-induced signaling protein nanoclustering contributes to cell polarity formation. (* co-corresponding author) Nature Communications, 11(1), pp.1-14.
- Yilun Zhu, Yuchi Qiu, Weitao Chen, Qing Nie, Arthur Lander. Scaling a Dpp morphogen gradient through feedback control of receptors and co-receptors. Developmental Cell, 53, no.6 (2020), pp.724-739.
Heyrim Cho
- H. Cho, A. Lewis, K. Storey, 'Bayesian Information-Theoretic Calibration of Radiotherapy Sensitivity Parameters for Informing Effective Scanning Protocols in Cancer', J Clin Med. 9, 2020
- H. Cho, K. Ayers, L. DePillis, Y-H. Kuo, J. Park, A. Radunskaya, R. Rockne, ‘Modeling acute myeloid leukemia in a continuum of differentiation states’, Lett. Biomath., 5, 2018
- H. Cho, D. Venturi, G. E. Karniadakis, ‘Numerical methods for high-dimensional probability density function equations', J. Comput. Phys. 305, 2016
Yat Tin Chow
- Y.T. Chow, J. Darbon, S. Osher, W. Yin, Algorithm for Overcoming the Curse of Dimensionality for State-dependent Hamilton-Jacobi equations, Journal of Computational Physics 387, pp. 376-409, 2019.
- H. Ammari, Y.T. Chow, J. Zou, Super-resolution in imaging high contrast targets from the perspective of scattering coefficients, Journal de Mathematiques Pures et Appliquees 111, pp. 192-226, 2018.
- Y.T. Chow, K. Ito, K. Liu, J. Zou, Direct sampling method for diffusive optical tomography, SIAM Journal of Scientific Computing 37(4), A1658–A1684, 2015.
Jia Gou
- Jia Gou, Lin Lin, Hans G. Othmer, A Model for the Hippo Pathway in the Drosophila Wing Disc, Biophys. J., 115(4), (2018), https://www.sciencedirect.com/science/article/pii/S0006349518307641 .
- Jia Gou, Michael J. Ward, An Asymptotic Analysis of a 2-D Model of Dynamically Active Compartments Coupled by Bulk Diffusion, J. Nonl. Sci., 26(4), (2016), https://link.springer.com/article/10.1007/s00332-016-9296-7 .
- Jia Gou, Yue Xian Li, Wayne Nagata, Michael J. Ward, Synchronized Oscillatory Dynamics for a 1-D Model of Membrane Kinetics Coupled by Linear Bulk Diffusion, SIAM J. Appl. Dyn. Sys., 14(4), (2015), https://epubs.siam.org/doi/abs/10.1137/15M1039122?af=R .
Jim Kelliher
- A characterization at infinity of bounded vorticity, bounded velocity solutions to the 2D Euler equations, Indiana University Mathematics Journal, 64(6), 1643-1666, 2015.
- Observations on the vanishing viscosity limit, Transactions of the American Mathematical Society, 369, 2003-2027, 2017. Published electronically 2 June 2016. Comment.
- With Elaine Cozzi, Well-posedness of the 2D Euler equations when velocity grows at infinity, Discrete & Continuous Dynamical Systems, 39(5), 2361-2392, 2018.
Amir Moradifam
Misha Potomkin
- Chi, H., Potomkin, M., Zhang, L., Berlyand, L. and Aranson, I.S., 2020. Surface anchoring controls orientation of a microswimmer in nematic liquid crystal. Communications Physics, 3(1), pp.1-9.
- Berlyand, L., Jabin, P.E., Potomkin, M. and Ratajczyk, E., 2020. A kinetic approach to active rods dynamics in confined domains. Multiscale Modeling & Simulation, 18(1), pp.1-20.
- Potomkin, M., Kaiser, A., Berlyand, L. and Aranson, I.S., 2017. Focusing of active particles in a converging flow. New Journal of Physics, 19(11), p.115005.
Russell Rockne
- Rockne RC, Hawkins-Daarud A, Swanson KR, Sluka JP, Glazier JA, Macklin P, Hormuth D, Jarrett AM, Lima EABDF, Oden J, Biros G, Yankeelov TE, Curtius K, Bakir IA, Wodarz D, Komarova N, Aparicio L, Bordyuh M, Rabadan R, Finley S, Enderling H, Caudell JJ, Moros EG, Anderson ARA, Gatenby R, Kaznatcheev A, Jeavons P, Krishnan N, Pelesko J, Wadhwa RR, Yoon N, Nichol D, Marusyk A, Hinczewski M, Scott JG. The 2019 Mathematical Oncology Roadmap. Physical Biology, vol. 16, no. 4, 2019 Apr 16. PMID: 30991381 PMCID: PMC6655440 DOI: 10.1088/1478-3975/ab1a09
- Rockne RC, Branciamore S, Qi J, Frankhouser DE, O’Meally D, Hua W-K, Cook G, Carnahan E, Zhang L, Marmom A, Wu H, Maestrini D, Wu X, Yuan Y-C, Liu Zheng, Wang LD, Forman S, Carlesso N, Kuo Y-H, Marcucci G. State-Transition Analysis of Time-Sequential Gene Expression Identifies Critical Points That Predict Development of Acute Myeloid Leukemia. Cancer Research 2020 Aug 1;80(15):3157-3169 PMID: 32414754 PMCID: PMC7416495 DOI: 10.1158/0008-5472.CAN-20-0354
- Abler D., Büchler P., Rockne R.C. (2019) Towards Model-Based Characterization of Biomechanical Tumor Growth Phenotypes. In: Bebis G., Benos T., Chen K., Jahn K., Lima E. (eds) Mathematical and Computational Oncology. ISMCO 2019. Lecture Notes in Computer Science, vol 11826. Springer, Cham. DOI: 10.1007/978-3-030-35210-3_6, ISBN 978-3-030-35209-7
Qixuan Wang
- Qixuan Wang*, Ji Won Oh*, Hye-Lim Lee, Anukriti Dhar, Tao Peng, Raul Ramos, Christian Fernando Guerrero-Juarez, Xiaojie Wang, Ran Zhao, Xiaoling Cao, Jonathan Le, Melisa A Fuentes, Shelby C Jocoy, Antoni R Rossi, Brian Vu, Kim Pham, Xiaoyang Wang, Nanda Maya Mali, Jung Min Park, June- Hyug Choi, Hyunsu Lee, Julien Legrand, Eve Kandyba, Jung Chul Kim, Moonkyu Kim, John Foley, Zhengquan Yu, Krzysztof Kobielak, Bogi Andersen, Kiarash Khosrotehrani, Qing Nie#, Maksim V Plikus#. "A multi-scale model for hair follicles reveals heterogeneous domains driving rapid spatiotemporal hair growth patterning." eLife, 6 (2017): e22772. [Link].
- Qixuan Wang*, William R. Holmes*, Julian Sosnik, Thomas Schilling, Qing Nie#. "Cell sorting and noise-induced cell plasticity coordinate to sharpen boundaries between gene expression domains." PLoS Computational Biology, 13.1 (2017): e1005307. [Link]
- Qixuan Wang# and Hans G. Othmer. "Computational analysis of amoeboid swimming at low Reynolds number." Journal of Mathematical Biology, 72.7 (2016): 1893-1926. [Link] [ArXiv]
Funding Opportunities
Research Grants
- NIH, National Institute of Biomedical Imaging and Bioengineering (NIBIB)Mathematical Modeling, Simulation and Analysis
- National Science Foundation, Applied Mathematics
- National Science Foundation, Mathematical Biology Program
- Joint NSF DMS/NIH NIGMS Initiative to Support Research at the Interface of the Biological and Mathematical Sciences
- National Science Foundation, Models for Uncovering Rules and Unexpected Phenomena in Biological Systems (MODULUS)
Support for Graduate & Undergraduate Students
Applied Math Degrees Information
Seminar Schedules
- ICQMB: https://icqmb.ucr.edu/news-weekly-seminar-conferences-and-special-events
- Partial Differential Equations & Applied Math: https://sites.google.com/ucr.edu/ucriverside-math-ampde-seminar/
Members of the Applied Math Group

Mark Alber
Director of ICQMB;
Department of Mathematics,
University of California, Riverside
Mark Alber is working on several interdisciplinary projects combining multi-scale mathematical modeling and experimentation. Mathematical and computer models allow researchers to perform virtual experiments that are currently impossible in the lab. Coupled with live imaging experiments and new image analysis methods, these experiments will yield insights into biological mechanisms governing organ formation in plants and animals and development of cancer in epithelial cell layers of the colon.Another collaborative project with University of Pennsylvania School of Medicine is on multi-scale modeling and empirical study of a mechanism limiting blood clot growth. Thrombosis is a major cause of death in the developed world and results from the growth of thrombi (blood clots forming within blood vessels) that restricts blood flow to vital organs. The project integrates multi-scale modeling and experiments to examine novel hypothesis related to the role of fibrin networks in processes halting thrombus growth. This will help physicians to estimate risk of thrombotic disease for an individual patient by identifying critical values of parameters of processes regulating thrombogenesis.
Selected publications:
1. Samuel Britton, Oleg Kim, Francesco Pancaldi, Zhiliang Xu, Rustem I. Litvinov, John W.Weisel, Mark Alber [2019], Contribution of nascent cohesive fiber-fiber interactions to the non-linear elasticity of fibrin networks under tensile load, Acta Biomaterialia 2019 May 30. pii: S1742-7061(19)30395-2. doi: 10.1016/j.actbio.2019.05.068. [Epub ahead of print].
2. Banwarth-Kuhn M., Nematbakhsh A., Rodriguez KW., Snipes S., Rasmussen CG., Reddy GV., Alber M. [2018], Cell-Based Model of the Generation and Maintenance of the Shape and Structure of the Multilayered Shoot Apical Meristem of Arabidopsis thaliana. Bull. Math. Biol. 2018 Dec 14. doi: 10.1007/s11538-018-00547-z. [Epub ahead of print]
3. Oleg V. Kim, Rustem I. Litvinov, Mark S. Alber and John W. Weisel [2017], Quantitative Structural Mechanobiology of Platelet-Driven Blood Clot Contraction, Nature Communications 8: 1274 (authors for correspondence: J.W. Weisel and M. Alber).

William Cannon
Computational Mathematics,
Pacific Northwest National Laboratory;
Adjunct Professor, Department of Mathematics,
University of California, Riverside
https://www.pnnl.gov/science/staff/staff_info.asp?staff_num=7055
Dr. William Cannon from the Pacific Northwest National Laboratory (PNNL) was appointed Adjunct Professor in the Department of Mathematics, UC Riverside. Dr. Cannon's Research Interests include: Computational biophysics, biochemistry and proteomics; Modeling and simulation including deterministic and stochastic simulation of metabolism; simulations of state; microbial metabolism; statistics, statistical mechanics and statistical proteomics data analysis; Cloud computing and high performance.
Dr. Cannon is author of more than 50 technical publications in modeling and simulation, data analysis and proteomics. His graduate work was in statistical thermodynamics in the laboratory of J. Andrew McCammon studying molecular recognition proteins using molecular dynamics and Monte Carlo methods. His graduate work was in the laboratory of Steven J. Benkovic where he worked in both experimental and computational enzymology. Before joining PNNL, Dr. Cannon spent time at Monsanto working on high-throughput transcriptome data analysis and network inference. Since joining PNNL, Dr. Cannon has worked on statistical methods for integrating proteomics data with models, the use of supercomputers to maximize the identification of peptides and proteins from high throughput mass spectrometry assays, and the modeling and simulation of metabolic pathways.
Researchgate: www.researchgate.net/profile/William_Cannon2
Weitao Chen
Department of Mathematics,
University of California, Riverside
https://sites.google.com/view/wtchen-mathbio/home
https://mathdept.ucr.edu/faculty/weitaochen.html
Dr. Weitao Chen is an applied mathematician specialized in numerical methods, scientific computing and computational systems biology. On the perspective of numerical methods and scientific computing, her research is focused on the development of high order methods for solving hyperbolic conservation laws, shape optimization of elliptic type eigenvalue problems and efficient solvers for reaction-diffusion systems in high dimensions. On the perspective of computational systems biology, her research interest is to understand fundamental principles in developmental biology, such as the mechanisms underlying pattern formation and growth control by developing multiscale mathematical models. Specifically, her research involves modeling spatiotemporal biochemical signaling network during cell polarization, e.g. yeast cells and pavement cells, or tissue growth such as Drosophila wing disc and shoot apical meristem in Arabidopsis Thaliana, as well as cell mechanical properties and stochasticity in signal transduction.

Heyrim Cho
Department of Mathematics,
University of California, Riverside
https://mathdept.ucr.edu/faculty/hcho.html
Dr. Cho's research interests and activities are in the areas of mathematical biology and uncertainty quantification. She is particularly interested in modeling multi-scale biological systems, and characterizing effects of the underlying uncertainty for comprehensive mathematical modeling and a better understanding of biological mechanisms. Her current projects include modeling problems in mathematical oncology to incorporate data arising from various scales including genetic data, cellular level, and tissue-scale imaging. She aims to use mathematical modeling for a better understanding of cancer progression and treatment and to further utilize the models in the clinic and in precision medicine.

Yat Tin Chow
Department of Mathematics,
University of California, Riverside
https://profiles.ucr.edu/app/home/profile/yattinc
Yat Tin Chow is an Assistant Professor in the Department of Mathematics. He received his Ph.D. in Mathematics from the Chinese University of Hong Kong. He comes to UC Riverside after being a CAM assistant adjunct professor in Department of Mathematics in UCLA. His major research direction is applied mathematics. Dr. Chow's current research interests includes resolution analysis and enhancement of imaging from boundary measurements of various physical quantities, e.g. electric current, acoustic wave, light intensity, etc. He is also interested in computational methods of medical imaging and tomography, e.g. Electrical Impedance Tomography. Dr. Chow's other fields of interest include both theoretical and numerical aspects of large scale optimization method, computations of control methods and conflict modeling in high dimensional systems, as well as transportation plans and games between large populations in the mean field, and different phenomena that arise from this setting.
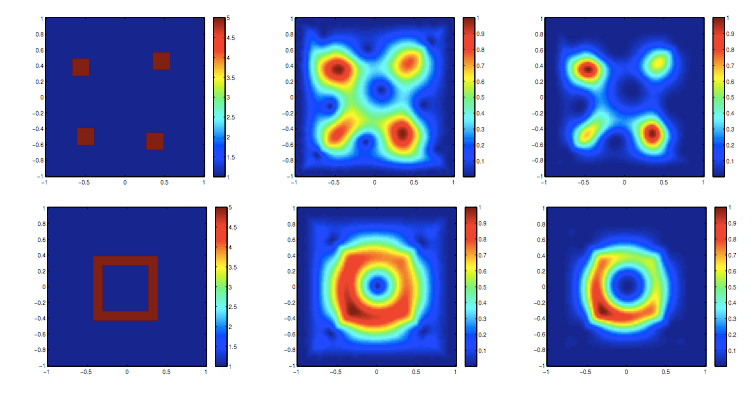

Jia Gou
Department of Mathematics,
University of California, Riverside
Dr. Gou's research interests are in the areas of mathematical biology and applications of dynamical systems. Her recent research focuses on understanding the growth control mechanisms by constructing and investigating models that describe cell signaling pathways and transport of molecules in tissues. She is also interested in analyzing mathematical models of spatial and temporal phenomena in biology, using techniques such as asymptotics and perturbation methods, and numerical simulations. One such model is related to a system of spatially segregated signaling cells coupled through a passive bulk diffusion field. Theoretical investigation reveals that such coupling is a robust mechanism for the initiation of synchronized oscillatory dynamics in the segregated cells. Quorum sensing phenomenon, collective behavior of cells in response to changes in their population size, is also observed in such system.

Jim Kelliher
Department of Mathematics,
University of California, Riverside
https://profiles.ucr.edu/app/home/profile/jamesk
https://math.ucr.edu/~kelliher/
Dr. Kelliher studies mathematical problems of fluid motion, especially singular limits involving the Navier-Stokes equations, Euler equations, and other equations of fluid mechanics. Much of his research has focused on the interaction of a nearly incompressible fluid, such as air or water, with a boundary. It is known that in a thin layer near the boundary, such a fluid makes a sharp transition from that of "free space" to that of a highly viscous fluid constrained by the boundary. A mathematically precise understanding of this transition, however, has not advanced far beyond that hypothesized by Ludwig Prandtl in 1905. Yet such an understanding is critical in many applications, including the design of aircraft wings and explaining why a breaking ball breaks.

Siting Liu
Department of Mathematics,
University of California, Riverside
Dr. Liu's research focuses on mathematical modeling and computational techniques, particularly in mean-field games and mean-field control models. She develops efficient computational methods that leverage machine learning and mesh-based techniques to solve partial differential equations. Her work spans various applications in data science, machine learning, and engineering, aiming to provide advanced modeling tools and practical solutions to complex, real-world problems.

Amir Moradifam
Department of Mathematics,
University of California, Riverside
Dr. Moradifam's research interests include Partial Differential Equations, Inverse Problems, Medical Imaging, and Mathematical Biology. He uses techniques from Mathematical Analysis and PDEs to answer fundamental questions about real life problems. In particular, Dr. Moradifam's research has recently been focused on the analysis of two new medical imaging modalities: Current Density Impedance Imaging (CDII) and photoacoustic tomography. CDII in the inverse problem of recovering the conductivity inside an object from the magnitude of the induced current in the interior. Such interior measurements of interior current could be obtained by Magnetic Resonance Imaging (MRI). In his work on photoacoustic tomography, Dr. Moradifam has been working on simultaneous determination of both the source of a wave and its speed in a medium from the measurements of the solution of the wave equation on the boundary. Dr. Moradifam has also had important contributions to the theory of Elliptic Partial Differential Equations. His breakthrough work on the Sphere Covering Inequality provided a solution to a 30-year old conjecture of A. Change and P. Yang (1987) about Nirenberg's problem on prescribing the Gaussian curvature on the sphere.

Mykhailo Potomkin
Department of Mathematics,
University of California, Riverside
http://personal.psu.edu/mup20/
Dr. Potomkin’s principal area of research is modeling, analysis and numerical simulation of problems involving differential equations (ordinary, stochastic and partial differential equations). His primary interest is on problems arising in Mathematical Biology and Soft Matter Physics. His recent work has been mostly devoted to active matter, with the focus on suspensions of micro-swimmers exhibiting autonomous directed motion, such as bacteria, motile spermatozoa, or bio-mimetic chemically driven particles. His research results include development and multi-scale analysis of the hierarchy of kinetic models capturing dynamics of confined suspensions, estimation of impact of micro-swimmers’ activity on macroscale properties of suspensions, as well as continuum approximations to systems of correlated interacting micro-swimmers. He is also interested in development and analysis of PDE models describing individual swimming at micro-scale.

Maziar Raissi
Department of Mathematics,
University of California, Riverside
Maziar Raissi is an Assistant Professor of Applied Mathematics at the University of California, Riverside. After receiving his Ph.D. in Applied Mathematics & Statistics, and Scientific Computations from the University of Maryland, College Park, he carried out his postdoctoral research in the Division of Applied Mathematics at Brown University. He then worked at NVIDIA in Silicon Valley as a Senior Software Engineer before moving to Boulder, CO where he was an Assistant Professor of Applied Mathematics at the University of Colorado Boulder. Dr. Raissi’s expertise lies at the intersection of Probabilistic Machine Learning, Deep Learning, and Data Driven Scientific Computing. He has been actively involved in the design of learning machines that leverage the underlying physical laws and/or governing equations to extract patterns from high-dimensional data generated from experiments.

Russell Rockne
Department of Computational and Quantitative Medicine,
Beckman Research Institute of City of Hope;
Department of Mathematics,
University of California, Riverside
https://www.cityofhope.org/people/rockne-russell
Russell Rockne, Ph.D., is an Assistant Professor in the Department of Computational and Quantitative Medicine within Beckman Research Institute of City of Hope. He also serves as director of the Division of Mathematical Oncology, with the goal of translating mathematics, physics and evolution-based research to clinical care.
The division, a part of the Irell & Manella Graduate School of Biological Sciences and the Beckman Research Institute of City of Hope, uniquely combines clinical care, scientific research and mathematical expertise to enhance the overall understanding of cancer development, growth, evolution and reaction to treatment. This work ultimately helps the care team to predict, control and thwart malignancy on both a global scale by improving evidence-based standards of care and an individual level by personalizing treatment using quantifiable patient and disease factors.

Qixuan Wang
Department of Mathematics,
University of California, Riverside
https://sites.google.com/ucr.edu/qixuanwang/
Dr. Wang’s research area is mathematical biology with main focuses on multi-scale modeling of complex developmental systems. She develops new mathematical models and computational tools to address questions in developmental systems. In particular, she uses mammalian hair follicles as a model system and develops multi-scale models to investigate the underlying control mechanisms of follicle growth and regeneration, the interplay between bio-chemistry and bio-mechanics in follicle development, and the communications among follicles which lead to coordinated follicle growth in different skin domains. She is also interested in developing computational methods and applying analysis in swimming micro-organisms in viscous flows. To answer questions from life sciences, she uses and develops a wide variety of tools including stochastic differential equations, dynamical system, scientific computing, asymptotic analysis and complex analysis.
Yiwei Wang
Department of Mathematics,
University of California, Riverside
https://sites.google.com/view/
Dr. Wang's research is primarily focused on mathematical modeling and scientific computing, with wide-ranging applications in physics, material science, biology, and data science. His current research interests include (1) Multiscale modeling and simulation of complex fluids, particularly those encountered in biological systems involving chemo-mechanical coupling and interactions; (2) Developing variational numerical methods for complex fluids models, including liquid crystals, phase-field, generalized diffusions, reaction-diffusion, and polymeric fluids; (3) Nonequilibrium thermodynamics and its application; (4) Machine learning, especially Bayesian methods.
Postdoctoral Associates
Dongwei Sun
Department of Bioengineering,
UC Riverside
Applied Math Graduate Students
Daniel Collister
Department of Mathematics,
University of California, Riverside
Cecilia Duran
Department of Mathematics,
University of California, Riverside

Mingye Gao
Department of Mathematics,
University of California, Riverside

Austin Hansen
Department of Mathematics,
University of California, Riverside

Tony Li
Department of Mathematics,
University of California, Riverside
Alireza Ramezani
Department of Physics,
University of California, Riverside
Jennifer Rangel-Ambriz
Department of Mathematics,
University of California, Riverside
Kevin Su
Department of Mathematics,
University of California, Riverside

Alysha Toomey
Department of Mathematics,
University of California, Riverside
Daniel Tran
Department of Mathematics,
University of California, Riverside
Minh Vu
Department of Mathematics,
University of California, Riverside
Applied Math Alumni

Mikhal Banwarth-Kuhn
Tenure-track Assistant Professor,
Department of Mathematics,
Cal State East Bay
Jolene Britton
Data Scientist,
Senior Specialist,
Southern California Edison (SEC)
Samuel Britton
Senior Member of Technical Staff,
The Aerospace Corporation,
El Segundo, CA

Joshua Buli
Senior Member of Technical Staff,
The Aerospace Corporation,
Los Angeles Metropolitan Area, CA

Christian Michael
Postdoctoral Associate,
University of Michigan
Kevin Tsai
Senior Member of Technical Staff,
Sensor Department of the Aerospace Corporation,
Diamond Bar, CA